重力の連続観測
グラフ1
観測は9月12日16時から9月19日16時までの7日間行いました。
測定は30分おきに行い、だいたい8時間、つまり16回の測定で測定者が交代しました。
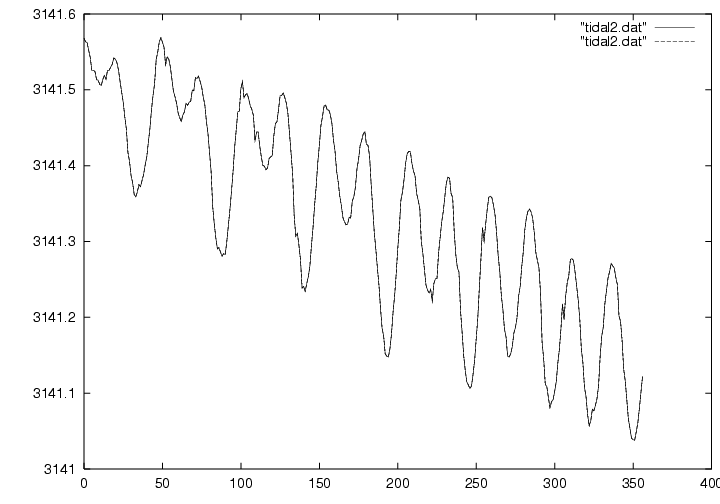
グラフ1は、オリジナルのデータをそのままグラフにしたものです。
横軸は測定開始からの積算時間(単位:分)、縦軸は読取値です。
読取値は、大きさとしてはおよそ mgal(参考として、測定に使用した場所の重力の絶対値は 979707.671 mgal)で、
測定に使用した重力計が LaCoste 重力計という相対重力計なので、重力の絶対値ではありません。
グラフ1より、オリジナルデータには重力計のドリフト(注1)による変化や、
測定者交代時の各測定者の読取癖による「はね」が含まれていることが分かります。
本演習の主目的は、この連続観測データを用い、tidal factor を求めることです。
tidal factor とは、地球がどれほど剛体からずれて「ブヨブヨ」であるかの指標で、
この値が1だと地球は完全に剛体である、ということになります。
実際には、約 1.2 程度で、地球は微妙に「ブヨブヨ」であることが分かります。
なぜ重力連続観測によりこのtidal factor を求めることができるのかについてはまたのちほど。
(注1) ドリフト
LaCoste重力計は一種のバネばかりで、バネののびによって重力の変化を測定する機械です。
そのため何もしなくてもバネ自身が勝手にのびていってしまうため、
重力の絶対的な変化以外にこうした見掛け上の変化が読取値には含まれます。
これをドリフトといい、解析する際には何らかの方法でこの効果を取り除いてからでないとうまくいきません。
グラフ2
解析は、オリジナルのデータに最小二乗法を使い、tidal factor、ドリフト係数、各測定者の読取癖に基づく
それぞれの定数(これを今は癖定数と呼ぶことにします)を求めました。
これにより、tidal factor は約 1.197 と見積もられました。
(実際には、オリジナルのデータにまだ幾つかの補正を施さなければならないのでこの値は暫定的なものです)
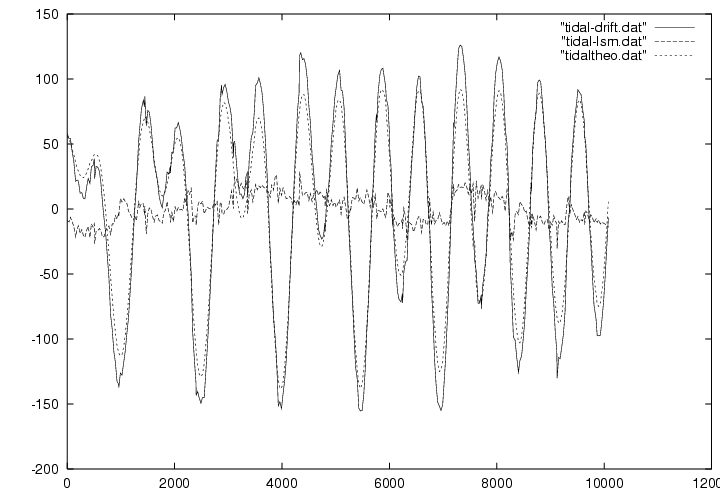
オリジナルのデータから、ドリフトによる効果および各癖定数を取り除いたものがグラフ2の実線で示されています。
やや分かりにくいですが、波線で示されているのは潮汐の理論値、点線で示されているのがそれらの差です。
グラフ1と同様、横軸には測定開始からの積算時間(分)、縦軸には潮汐による重力の変化分(単位:μgal)で
グラフを書いています。グラフ2をみると、実線が波線よりもやや大きな振幅を持つのが分かりますが、
これが地球が弾性体である証拠、すなわち tidal factor が1より大きい証拠です。
残差を見る限り何らかの変動がまだあるように思えます。
今回は「ドリフトは線型である」と仮定して解析を行ったので、もしかしたらこの仮定に誤りがあるかもしれません。
今後に期待してください。
グラフ3
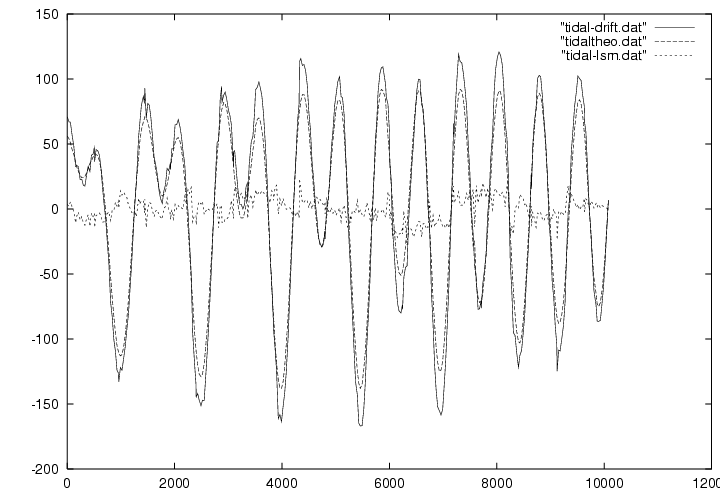
グラフ 2は、重力計のドリフトは時間的に線型であるとして観測方程式をつくり、
最小二乗法により tidal factor、各癖定数、ドリフト係数を求めた時の補正値のグラフですが、
グラフ 3 はドリフトは時間的に二次関数であるとして tidal factor、ドリフト係数(二つ)、各癖定数を求めたときのグラフです。
最初の方法では、tidal factor は 1.197 +- 9*10^(-3)であったのに対し、
今回の方法では、1.203 +- 7*10^(-3) と若干よい値に近づいています。
先の方法の時には、残差にまだ周期的な変化が見られましたが、今回はそれも少なくなっています。
しかし、決定的な違いがあるようには見えません。ドリフトは高次であると仮定すればするほど、いい値になるのは当然です。
さらに残差を詳しく解析するためには、気圧や気温などのデータを加えて解析しないとだめだと思われます。
グラフ4
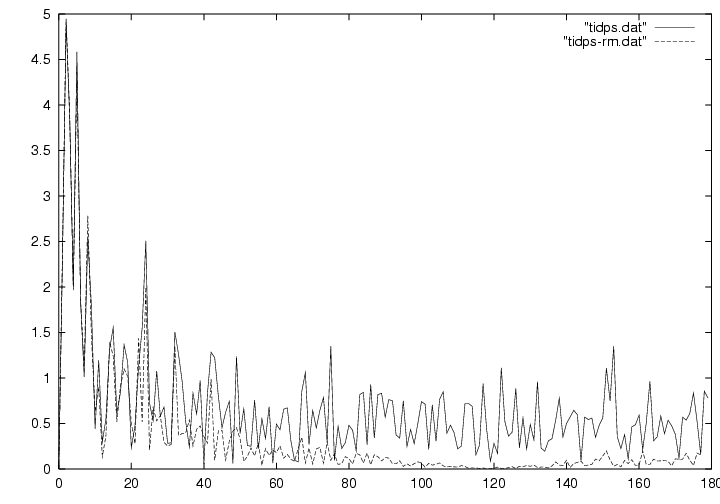
グラフ 4 は、方法2によって得られた残差に対し、フーリエ解析をしたときの結果です。
実線は、残差に対してそのままフーリエ解析をした結果、
波線は、5 データずつ(2時間30分)移動平均をしたあとにフーリエ解析をした結果です。
横軸は波数、縦軸は振幅です。移動平均をかけているため、波線のグラフは波数が多い方は振幅が小さくなっています。
振幅の単位は μgal なので波数が大きい方は振幅が小さくなっています。
実際、波数が大きい方は振幅が 1μgal 程度なので、
今回の測定においては測定者の未熟さに基づく測定誤差でないかと思われます。
しかし、波数が5以下の波は振幅が数μgal 程度あるものもあるので、
これには何らかの物理的解釈ができるかもしれません(気圧や、気温との関係)。
この文はまだ暫定的なものであり、誤りが存在するかもしれませんが、そのうち発見次第訂正していきます。
Mail to:小林佑輝