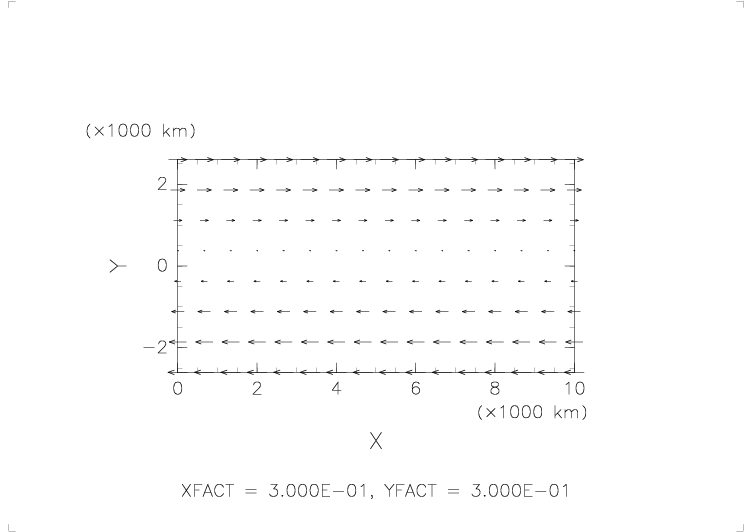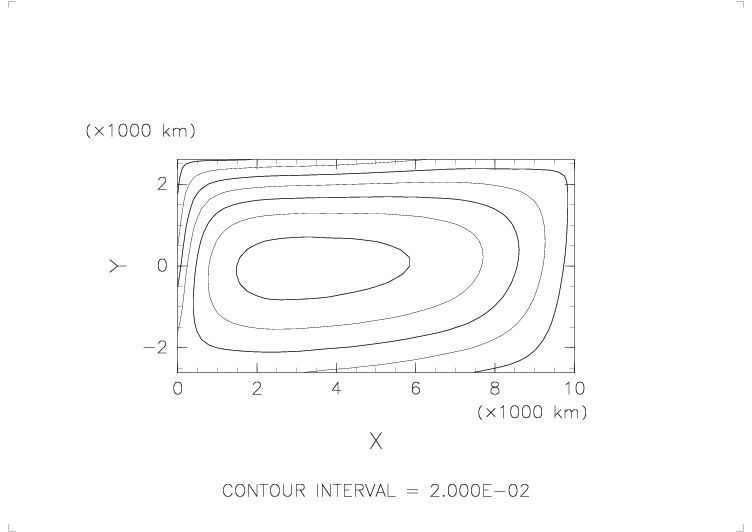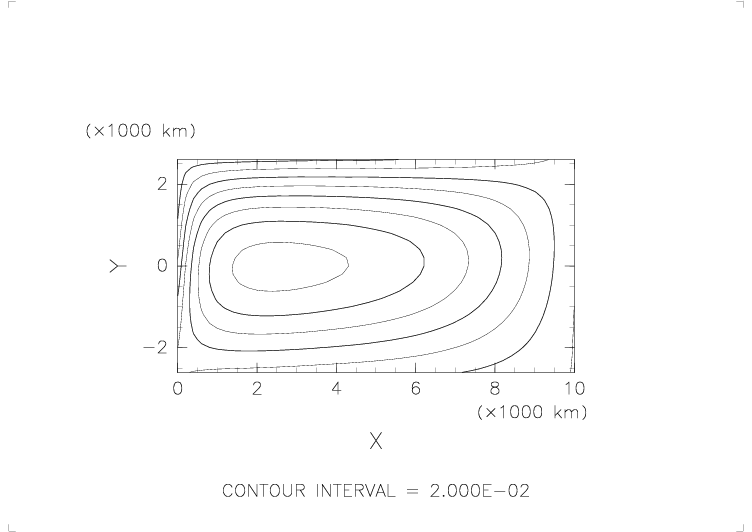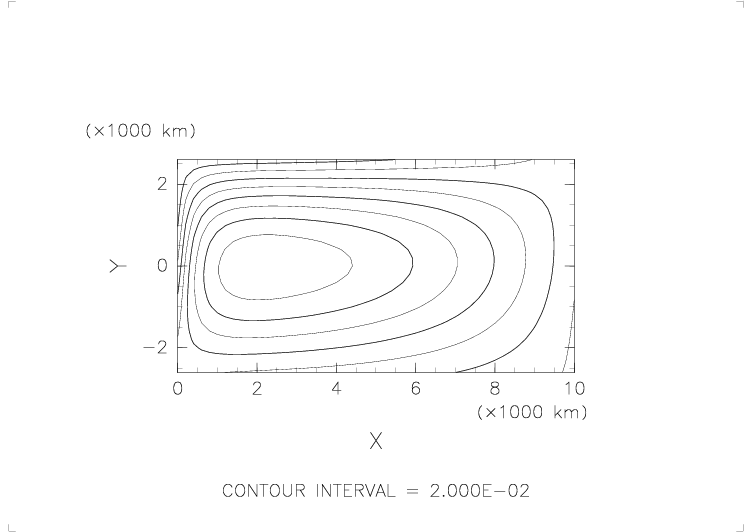
流向・流速
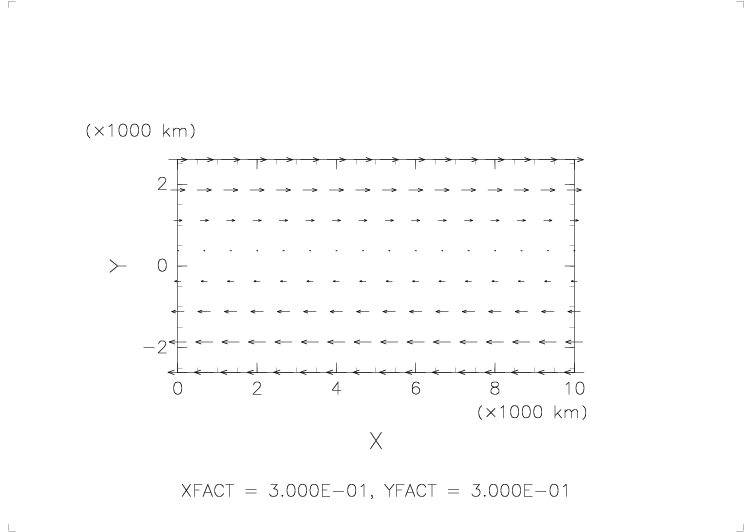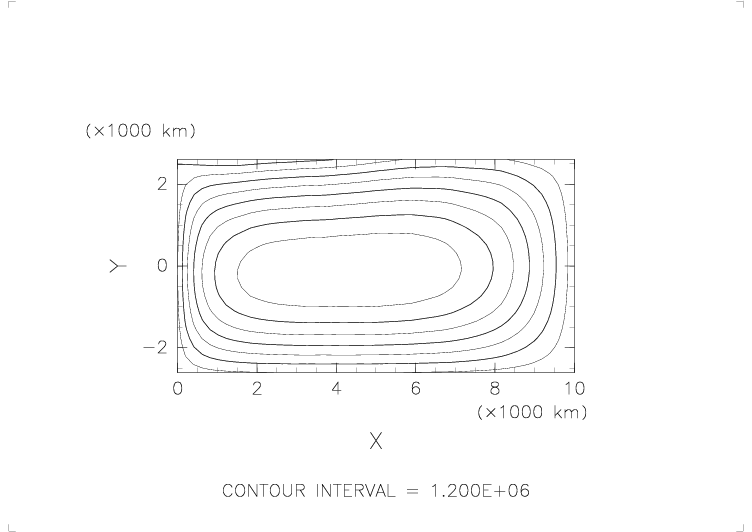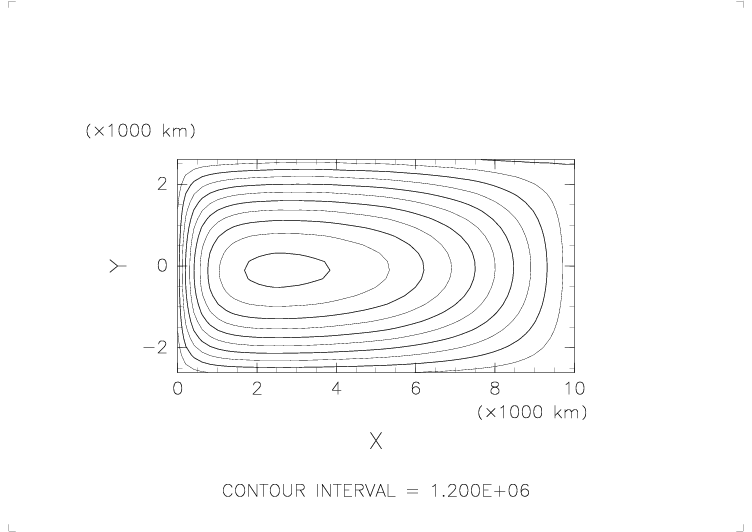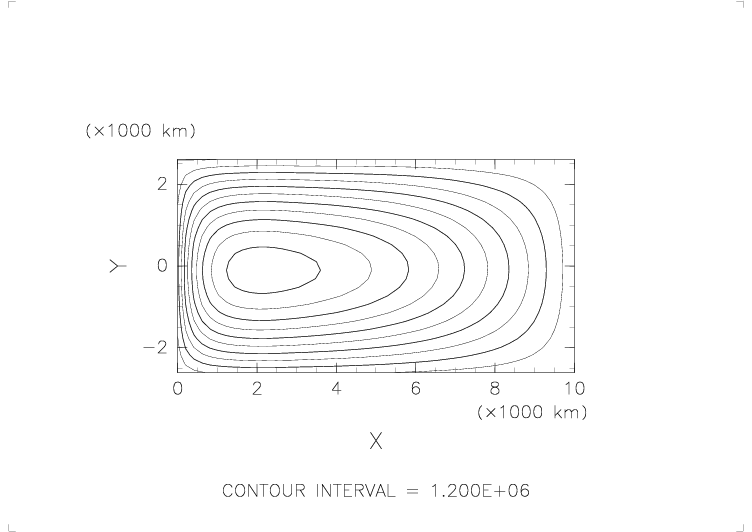
アニメの最初に出てくるパターンの風(風応力)を定常的に与え続けた場合の海面高と流量関数の変化。
定常的に与えた風(風応力)は、中緯度亜熱帯近辺、すなわち偏西風と貿易風(東風)を考え、
y > 0 では西風( x の正方向)、y < 0 では東風( x の負方向)である。正確には、
τx = 0.1 sin(πy/2500) (N/m^2)
τy = 0
である。
- 開始後すぐの海面はだいたい風下側で盛り上がり、風上側でへこんでいる。
しかし、時間が経つにつれ風下側の海面の盛り上がりが海洋の中央付近にはり出してくる。 - そのうち、海洋中央部が盛り上がり、その周辺部がへこんでいるというパターンに落ち着く。
- そのパターンは基本的にはくずれないが、盛り上がりの中心がだんだん西側に移動してくる。
それにともない、西側の境界で流量関数の等値線が密になってくる。
1 は、コリオリパラメーター f を f = 0 とおいたときと同じ立ち上がりである。
これは、1のパターンは実験開始からのごく短時間のパターンであり、
短時間の現象には地球の回転があまりきかないということとうまく合致する。
2 は、海面での摩擦があるためのエクマン層輸送による効果であると思われる。
エクマン層輸送は、風応力の方向に対し45度の角度を持つ。
つまり、風の向きから 45 度の方向に流れが生じているとも言える。
流線関数にはうまくあらわれていないが、これはエクマン層の流速が地衡流成分に比べて小さいためである。
すでにこの時、圧力勾配力とコリオリ力がほぼ釣り合った地衡流が形成されているのが、流量関数の分布からも分かる。
3 は、コリオリパラメーターが f = β y と y 方向に対し変化することにより、
海面の盛り上がりがロスビー波として伝わっていく過程であると思われる。
このロスビー波によって海洋に与えられた風応力の情報は西側境界まで伝わり、西岸境界流を形成するものと思われる。
領域の一番東端から出発したロスビー波が西側に到達するまで、海面高度および流量関数の値は時間変化し、
西側に達した時点で定常になる(実験3参照)。
このアニメでは、その時間まで絵がないので分からない。